David Alvarez-Melis

(he/him/his)

Assistant Professor, Harvard University (SEAS)

150 Western Av. #2-332 Allston MA 02134

[three initials]@seas.harvard.edu

Word Translation with Optimal Transport

OT-based approaches to fully unsupervised bilingual lexical induction

TL;DR: Unsupervised word translation can be cast as matching vectors across word embedding spaces. Optimal Transport is a neat, principled way to compute optimal matchings across metric domains, but it’s not directly applicable to this task (see below). We propose two approaches (this one and this one) to overcome this.


Background

Cross-lingual or cross-domain correspondences play key roles in tasks ranging from machine translation to transfer learning. Recently, purely unsupervised methods operating on monolingual embeddings have become effective alignment tools. Current state-of-the-art methods, however, involve multiple steps, including heuristic post-hoc refinement strategies. Optimal Transport provides a principled, compact and well-understood optimization approach to the problem of finding correspondences across objects. However, OT cannot be applied directly, as it assumes that the two spaces are registered, i.e., that meaningful distances can be computed across them. This is not the case for word embeddings, as they are estimated in a relative manner (based on inner products and distances), leaving, e.g., an overall rotation unspecified. To solve this challenge, we rely on two generalizations of optimal transport that allow it to operate on unregistered spaces: the Gromov-Wasserstein distances (Memoli, 2011) and a novel framework for endowing the OT objective with invariance to rotations.

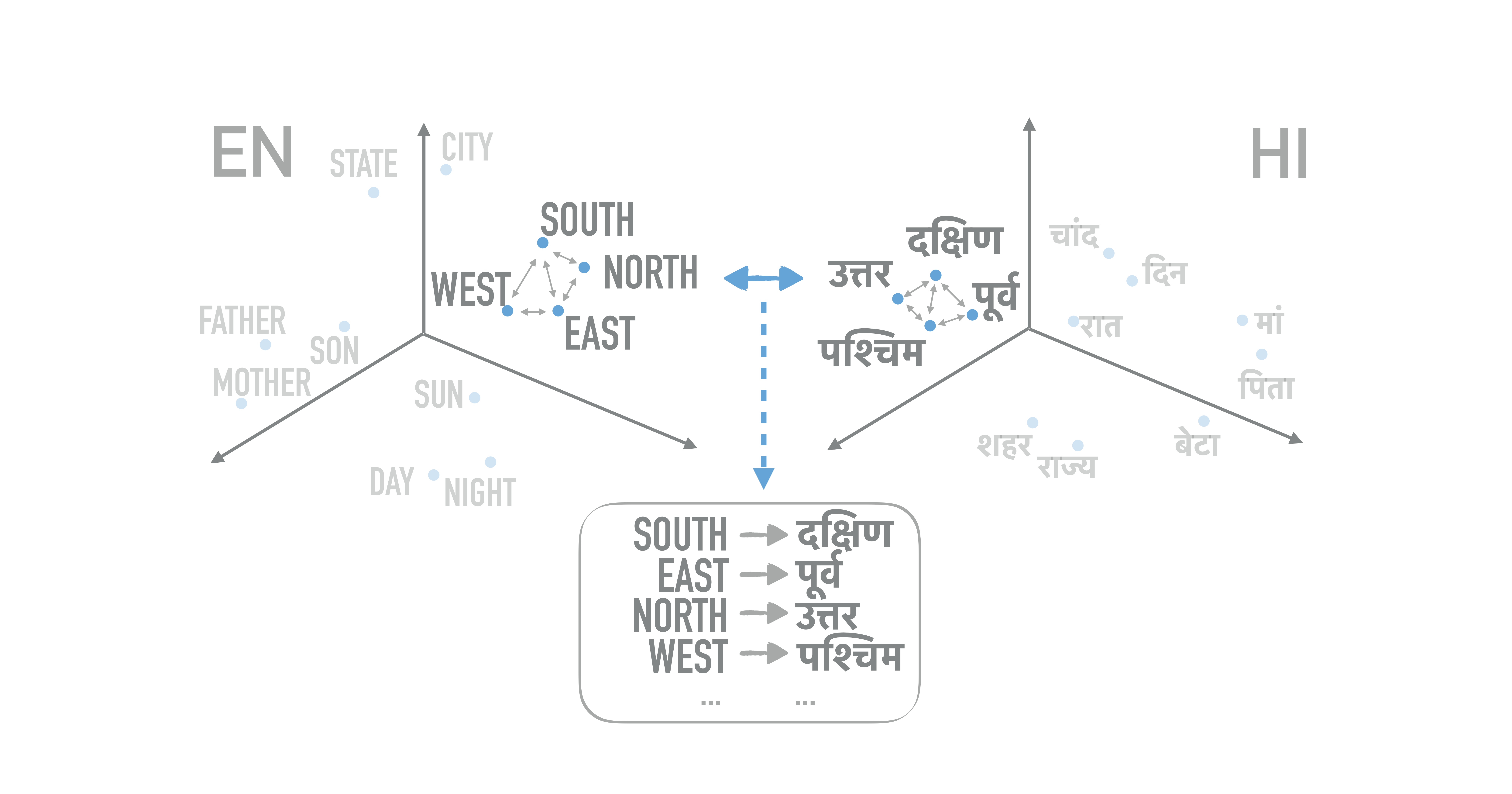
Although the absolute position of word vectors is meaningless, their geometry is similar across languages, which can be used to infer correspondences across word embedding spaces. OT offers an elegant framework to do so.
Although the absolute position of word vectors is meaningless, their geometry is similar across languages, which can be used to infer correspondences across word embedding spaces. OT offers an elegant framework to do so.


First Approach: Using the Gromov-Wasserstein Distance

The Gromov-Wasserstein distance (Mémoli, 2011) generalizes OT by directly comparing the metric spaces defined by the embeddings, instead of samples across the spaces. In other words, this framework operates on distances between pairs of points calculated within each domain and measures how these distances compare to those in the other domain. Thus, it requires a weaker but easy to define notion of distance between distances, and operates on pairs of points, turning the problem from a linear to a quadratic one.

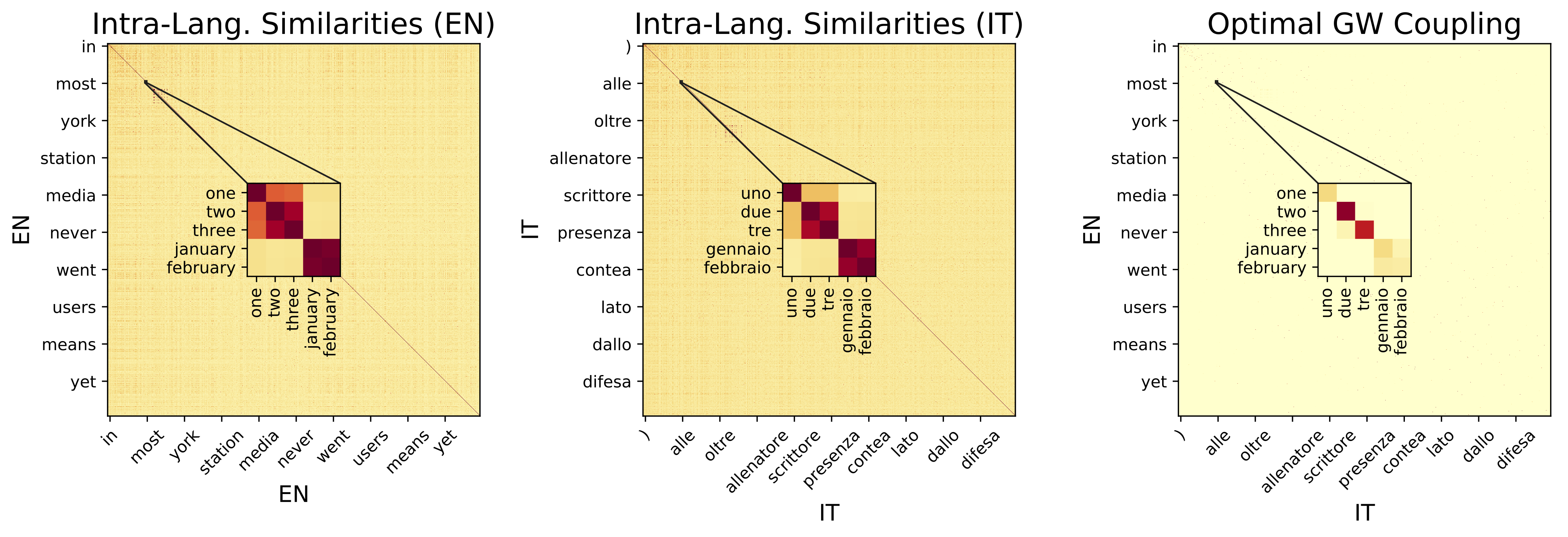
The Gromov-Wasserstein distance is well suited for the task of cross-lingual alignment because it relies on <i>relational</i> rather than <i>positional</i> similarities to infer correspondences across domains. Computing it requires two intra-domain similarity (or cost) matrices (left & center), and it produces an optimal coupling of source and target points with minimal discrepancy cost (right).
The Gromov-Wasserstein distance is well suited for the task of cross-lingual alignment because it relies on relational rather than positional similarities to infer correspondences across domains. Computing it requires two intra-domain similarity (or cost) matrices (left & center), and it produces an optimal coupling of source and target points with minimal discrepancy cost (right).


Second Approach: Using Optimal Transport with Invariances

We endow the OT objective with invariance to rotations, by using our framework of Optimal Transport with Invariances. Further details provided in that project’s page.

Relevant Publications:

  1. Alvarez-Melis and Jaakkola. “Gromov-Wasserstein Alignment of Word Embedding Spaces”, EMNLP 2018.
  2. Alvarez-Melis, Jegelka and Jaakkola. “Towards Optimal Transport with Global Invariances”, AISTATS 2019.
David Alvarez-Melis