David Alvarez-Melis | Dataset Distances and Dynamics

Dataset Distances and Dynamics

A principled framework to compare and transform labeled datasets

TL;DR: An notion of distance between labeled datasets based on optimal transport, which is highly predictive of model transferability across tasks, and which can be used to formalize a framework for dataset optimization.

See a detailed and interactive deep-dive post on the OTDD in the MSR Blog.

Summary

The notion of distance between tasks or datasets is crucial in various settings in machine learning that involve transferring knowledge across domains, such as domain adaptation and meta-learning. Current methods to quantify such distances are often heuristic, make strong assumptions on the datasets, and many require training a large deep learning model on each dataset compared. Our recent work [1] proposes an alternative notion of distance between datasets that (i) has a solid theoretical footing in OT, (ii) is model-agnostic, (iii) does not involve training, and—crucially—can compare datasets even if their label sets are completely disjoint, the first dataset distance that allows for this. Thus, it can be used to compare, e.g., a dataset of handwritten digits with a dataset of images of cars, despite their categories being completely unrelated. Besides enabling meaningful comparison of seemingly incomparable datasets, this optimal transport dataset distance (OTDD) strongly correlates with transferability of classifiers across domains. This demonstrates its promise as a tool to automatize dataset selection for transfer learning—a critical step of ML in practice.

While valuable in its own right, the OTDD is even more useful because of what it enables. By equipping the space of labeled datasets with a metric, it opens the door to import to this setting notions that can only—or at least, more easily—be defined on metric spaces. An intriguing example of this is (numerical) optimization, the back-bone of machine learning and many other computational fields. Performing optimization over datasets would be an appealing approach to various data-centric problems that cannot be naturally addressed with the current model-centric optimization paradigm in ML, such as finding optimal ways to preprocess datasets or transforming them to enforce certain (e.g., privacy) constraints. Our recent work [2] takes initial steps towards this goal, unifying various data-centric problems under a common framework of dataset optimization, which is formalized using ideas from applied mathematics, in particular gradient flows and differential equations. We show, for example, how this method can be used to transform a ‘source’ dataset (e.g., medical imaging) so that a classifier trained on a completely different dataset (e.g., photos of objects) can be used, with high accuracy, on the source dataset without modifying the model at all.

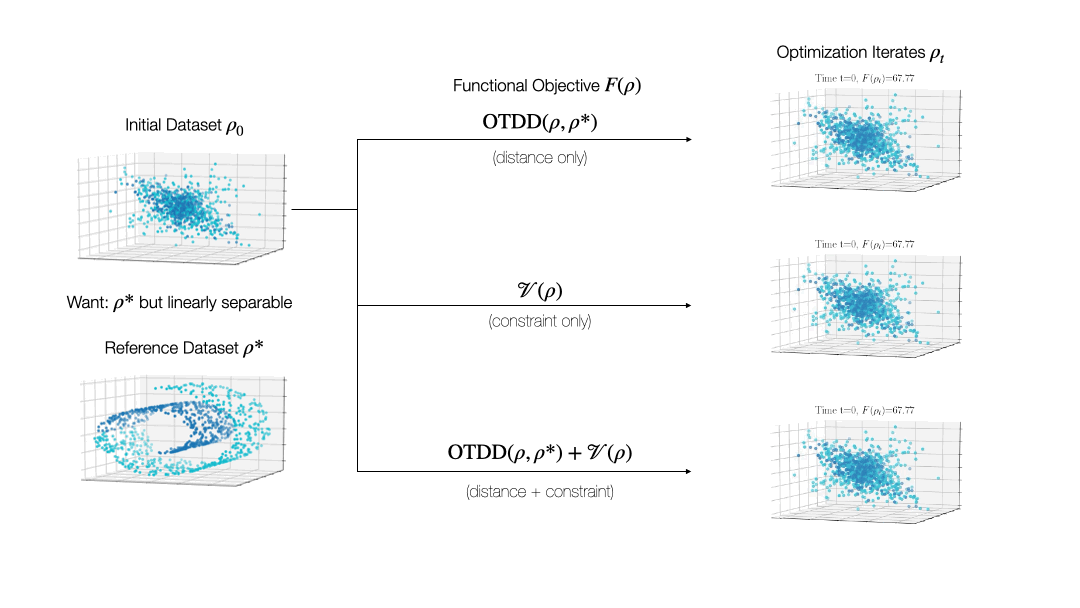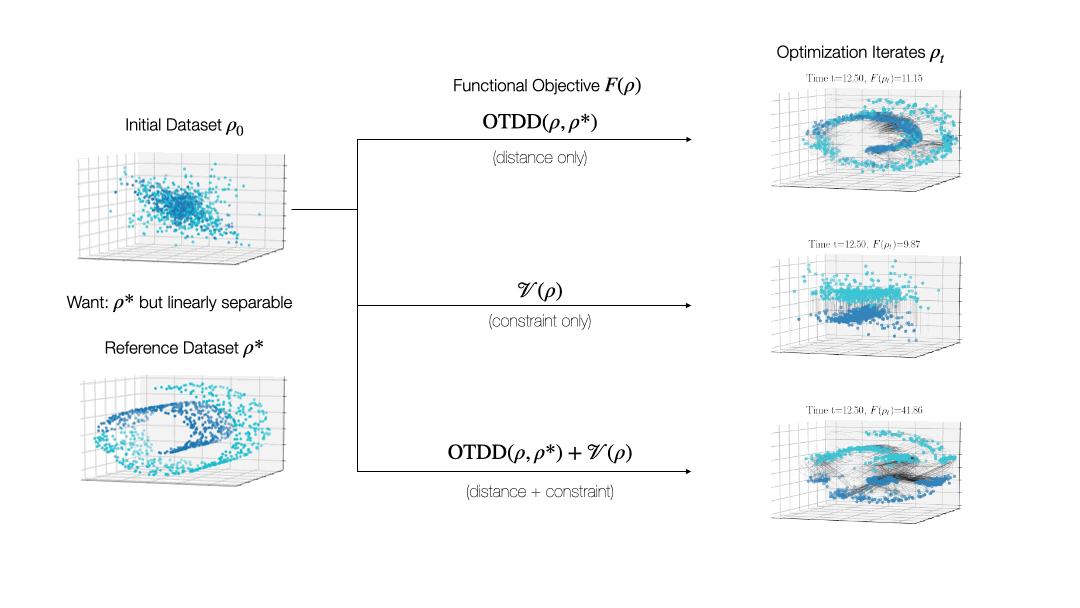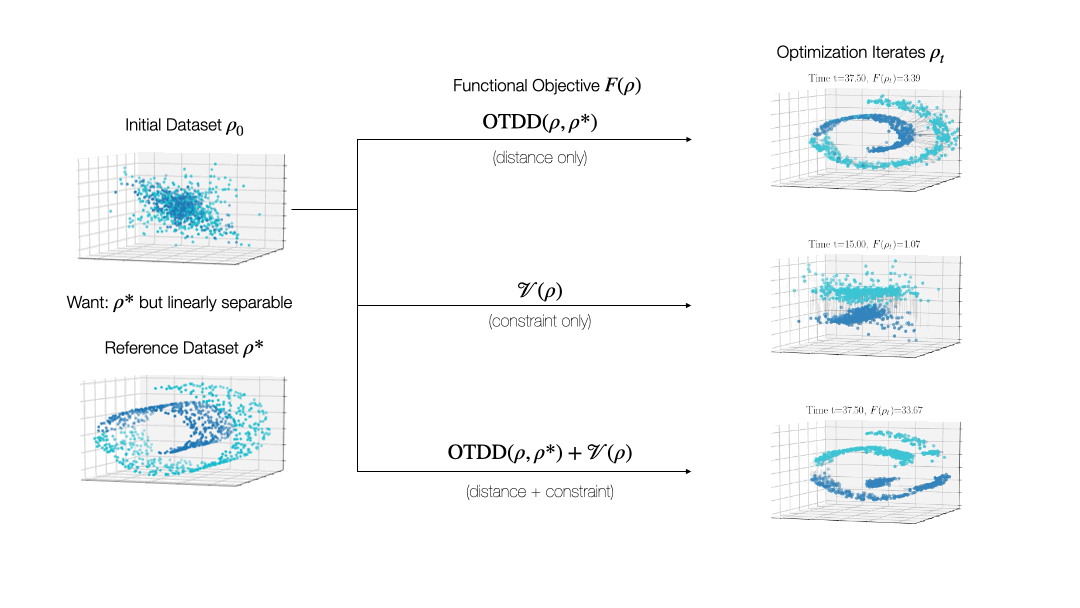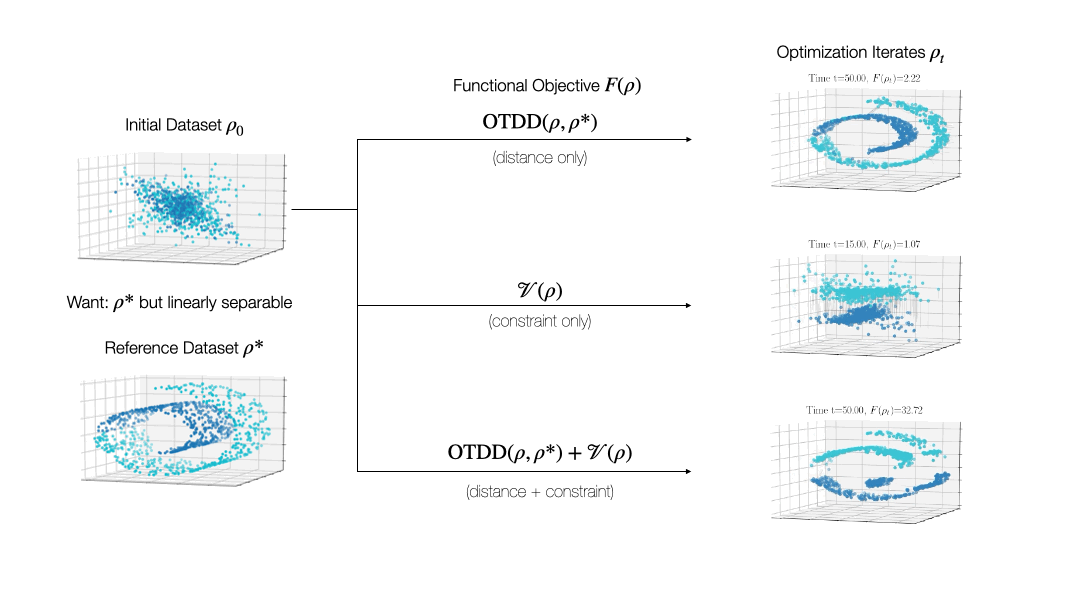
Dataset 'Shaping'. Our framework allows for simple and principled transformation of classification datasets by following the gradient flow of a functional objective, such as: similarity to a
reference dataset (shown here as $\mathrm{W}(\cdot, \rho^*)$ via OTDD), a function enforcing linear separability (shown here as $\mathcal{V}(\rho)$), or a combination thereof. — Dataset 'Shaping'. Our framework allows for simple and principled transformation of classification datasets by following the gradient flow of a functional objective, such as: similarity to a reference dataset (shown here as $\mathrm{W}(\cdot, \rho^*)$ via OTDD), a function enforcing linear separability (shown here as $\mathcal{V}(\rho)$), or a combination thereof.

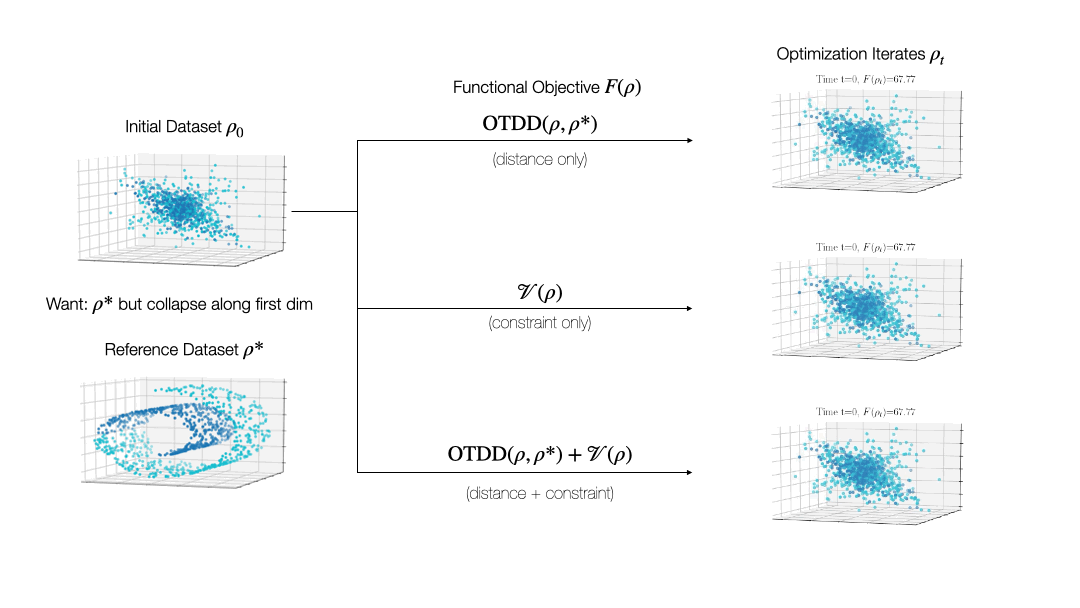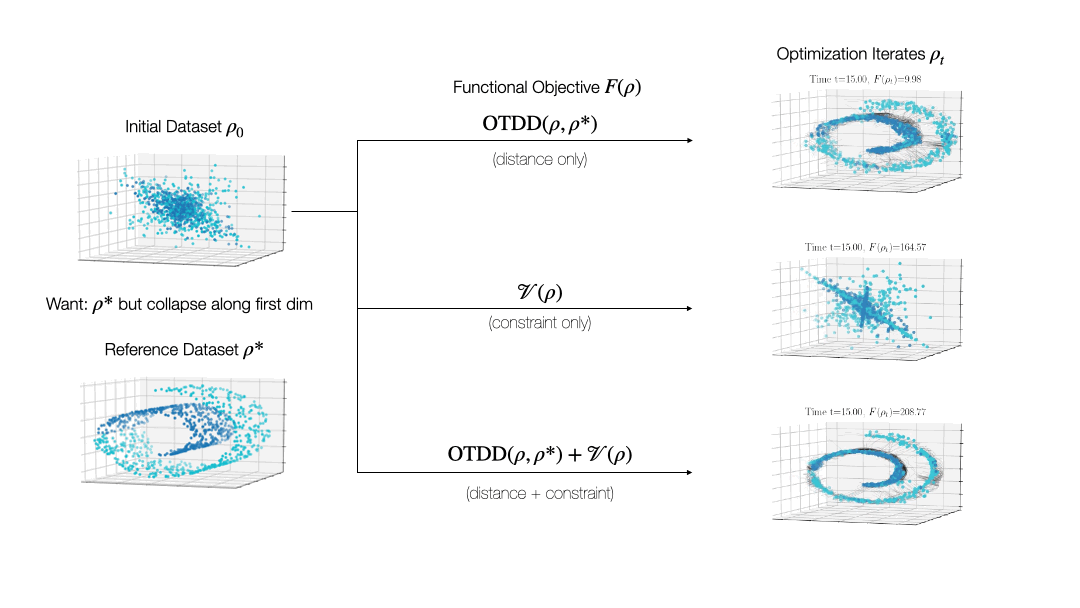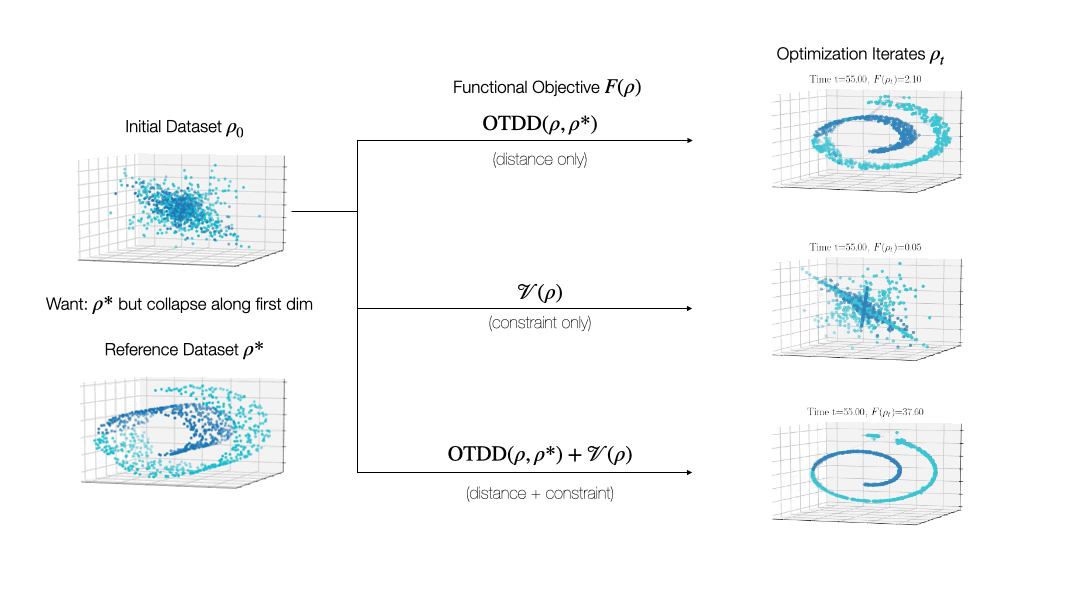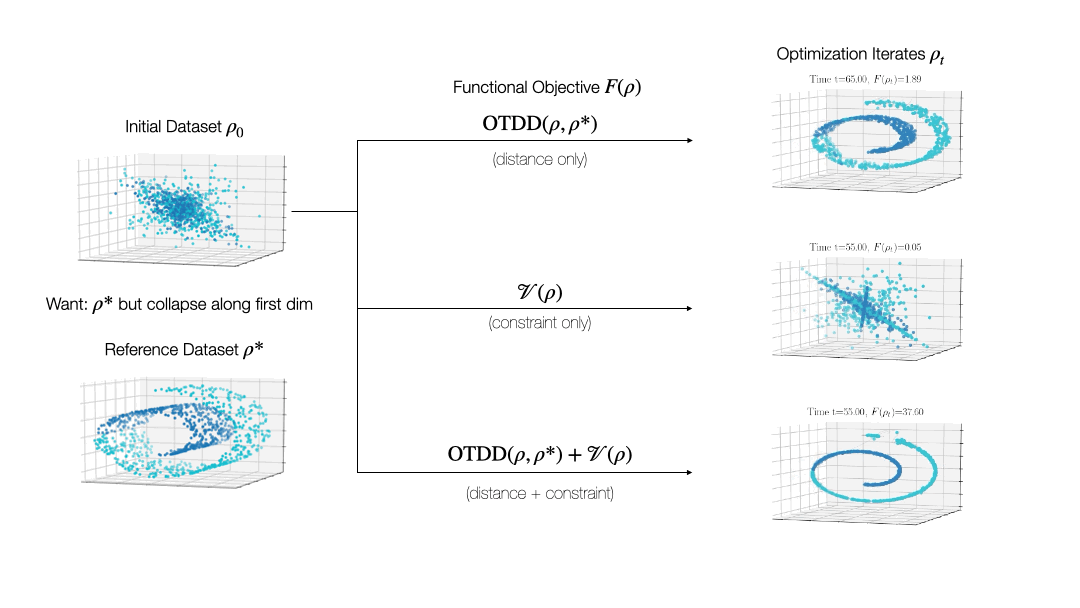
**Similar to above, but now the constraint-imposing functional $\mathcal{V}(\rho)$ enforces collapse along a given dimension, which could be used to obfuscate certain private attributes in a dataset.**

Relevant Publications:

Alvarez-Melis and Fusi. “Geometric Dataset Distances via Optimal Transport”, NeurIPS 2020.
Alvarez-Melis and Fusi. “Gradient Flows in Dataset Space”, ICML 2021.
Alvarez-Melis, Schiff & Mroueh. “Gradient Flows in Dataset Space”, arXiv 2021.